A Gentle Introduction To The Art Of Mathematics Pdf
Disclaimer: this is a summary of section 4.3 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.
Union and Intersection
We'll continue to develop the correspondence between logic and set theory. Take note of the following correspondence: (set theory symbols are just rounded mnemonic for the correspondence)
| | |
|---|---|
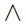 | 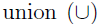 |
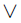 | 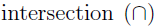 |
Given some open sentences P(x) and Q(x), the union of the corresponding truth sets Sp and Sq is defined by,
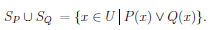
The union of more than two sets is expressed using a big union symbol. For instance, a family of real intervals defined by I_n = (n, n + 1] can be expressed as
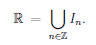
The intersection of two sets is conceptualized as "what they have in common" but the precise definition is found by considering conjunctions,
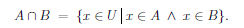
There is also a big version of the intersection symbol.
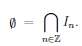
Summary:
| | |
|---|---|
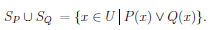 | 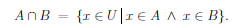 |
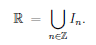 | 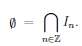 |
Negation
Negation in logic corresponds to complementation in set theory. The complement of a set is the set of all things that aren't in the set. It can be represented as follow,
| | |
|---|---|
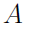 | 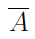 or or 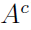 |
In thinking about complementation one quickly sees why the importance of working within a well-defined universal set is stressed. Many people think that the main reason for working within a fixed universal set is that we then have well-defined complements. The real reason that we accept this restriction is to ensure that both membership criteria, the set and its complement, are decidable open sentences.
Every rule we've learned in chapter 2 has a set-theoretic equivalent. These set-theoretic versions are expressed using equalities (i.e. the symbol = in between two sets) which is actually a little bit funny if you think about it. We normally use = to mean that two numbers or variables have the same numerical magnitude.
The table below shows the rules governing the interaction between the set-theoretic operations
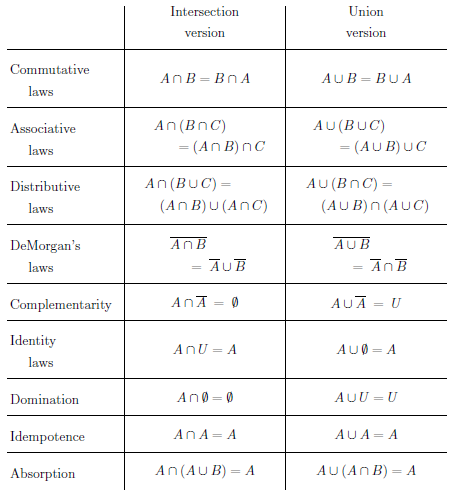
There are some notions within the set theory that don't have any clear parallels in logic. One of these is essentially a generalization of the concept of "complements". One can think of the complement of A as being the difference between the universal set U and the set A. The difference between two sets is written,
| Set Difference in Symbols | Set Difference in English |
|---|---|
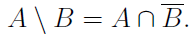 | Those elements of A that aren't in B |
(In some books, the difference of sets is defined first and then complementation is defined by 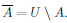 )
)
Symmetric Difference
Note that the difference of sets is not a commutative operation. In symbols, we have
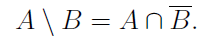
One can actually define an operation that acts somewhat like the difference, but that is commutative, this is known as the symmetric difference denoted by a triangle (greek delta),
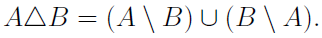
Exercise
To end this section, we will try to explore this exercise from the book.
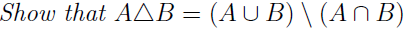
The two-column proof of this exercise is given as follows,
| | |
|---|---|
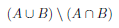 | 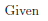 |
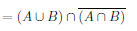 | 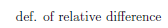 |
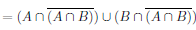 |  |
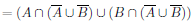 | 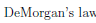 |
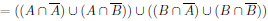 | 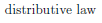 |
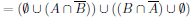 | 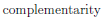 |
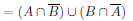 | 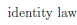 |
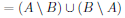 | 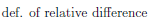 |
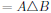 | 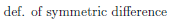 |
- A Gentle Introduction to the Art of Mathematics by Joe Field


A Gentle Introduction To The Art Of Mathematics Pdf
Source: https://steemit.com/mathematics/@sinbad989/a-gentle-introduction-to-mathematics-set-operations
Posted by: jenkinsenswer.blogspot.com

0 Response to "A Gentle Introduction To The Art Of Mathematics Pdf"
Post a Comment